2025

Estimation of covariance eigenvalues in high dimensions with different methods: the sample covariance matrix (SCM, red), the Ledoit-Wolf estimator (LW, orange) and our proposed algorithm based on eigengap sparsity (ESCP, green). The estimation error is much lower with our method.
Eigengap Sparsity for Covariance Parsimony
Tom Szwagier, Guillaume Olikier and Xavier Pennec
Covariance estimation is a central problem in statistics. An important issue is that there are rarely enough samples n to accurately estimate the p(p+1)/2 coefficients in dimension p. Parsimonious covariance models are therefore preferred, but the discrete nature of model selection makes inference computationally challenging. In this paper, we propose a relaxation of covariance parsimony termed ”eigengap sparsity” and motivated by the good accuracy–parsimony tradeoffs of eigenvalue-equalization in covariance matrices. This penalty can be included in a penalized-likelihood framework that we propose to solve with a projected gradient descent on a monotone cone. The algorithm turns out to resemble an isotonic regression of mutually-attracted sample eigenvalues, drawing an interesting link between covariance parsimony and shrinkage.
2025

Nested subspace learning with flags
Tom Szwagier and Xavier Pennec
Many machine learning methods look for low-dimensional representations of the data. The underlying subspace can be estimated by first choosing a dimension q and then optimizing a certain objective function over the space of q-dimensional subspaces (the Grassmannian). Trying different q yields in general non-nested subspaces, which raises an important issue of consistency between the data representations. In this paper, we propose a simple and easily implementable principle to enforce nestedness in subspace learning methods. It consists in lifting Grassmannian optimization criteria to flag manifolds (the space of nested subspaces of increasing dimension) via nested projectors. We apply the flag trick to several classical machine learning methods and show that it successfully addresses the nestedness issue.
2025

Parsimonious Gaussian mixture models with piecewise-constant eigenvalue profiles
Tom Szwagier, Pierre-Alexandre Mattei, Charles Bouveyron and Xavier Pennec
We introduce a new family of parsimonious GMMs with piecewise-constant covariance eigenvalue profiles. These extend several low-rank models like the celebrated mixtures of probabilistic principal component analyzers, by enabling any possible sequence of eigenvalue multiplicities. To address the notoriously-challenging issue of jointly learning the mixture parameters and hyperparameters, we propose a componentwise penalized EM algorithm, whose monotonicity is proven. We show the superior likelihood-parsimony tradeoffs achieved by our models on a variety of unsupervised experiments: density fitting, clustering and single-image denoising.
2024

The curse of isotropy: from principal components to principal subspaces
Tom Szwagier and Xavier Pennec
We raise an important issue (the curse of isotropy) about the interpretation of principal components with close eigenvalues. They may indeed suffer from an important rotational variability, which is a pitfall for interpretation. Through the lens of a probabilistic covariance model parameterized with flags of subspaces, we show that the curse of isotropy cannot be overlooked in practice. In this context, we propose to transition from ill-defined principal components to more-interpretable principal subspaces. The final methodology (principal subspace analysis) is extremely simple and shows promising results on a variety of datasets from different fields.
2023

Rethinking the Riemannian Logarithm on Flag Manifolds as an Orthogonal Alignment Problem
Tom Szwagier and Xavier Pennec
In this work, we exploit the homogeneous quotient space structure of flag manifolds and rethink the geodesic endpoint problem as an alignment of orthogonal matrices on their equivalence classes. The relaxed problem with the Frobenius metric surprisingly enjoys an explicit solution. This is the key to modify a previously proposed algorithm. We show that our explicit alignment step brings drastic improvements in accuracy, speed and radius of convergence, in addition to overcoming the combinatorial issues raised by the non-connectedness of the equivalence classes.
2022

Manifold learning
Elodie Maignant, Xavier Pennec, Alain Trouvé
In this work, we review popular manifold learning methods relying on the notion of neighbour graph (Laplacian Eigenmaps, Isomap, LLE, t-SNE) with a particular focus on Locally Linear Embedding (LLE). This includes:
– A deeper analysis of the different methods [hal-03909427].
– Comparative studies on symptomatic and shape analysis examples.
– The generalisation of the methods to manifold-valued data.

Graph Alignment Exploiting the Spatial Organisation Improves the Similarity of Brain Networks
Anna Calissano, Samuel Deslauriers-Gauthier, Theodore Papadopoulo, Xavier Pennec.
Can the structural and functional properties of a specific brain region of an atlas be assumed to be the same across subjects? In [hal-03910761] we addressed this question by looking at the network representation of the brain, with nodes corresponding to brain regions and edges to their structural relationships. We perform graph matching on a set of control patients and on parcellations of different granularity to measure the connectivity misalignment between regions. The graph matching is unsupervised and reveals interesting insight on local misalignment of brain regions
across subjects as shown in the figure.
The Currents Space of Graphs
James Benn, Anna Calissano, Stephen Marsland, Xavier Pennec.
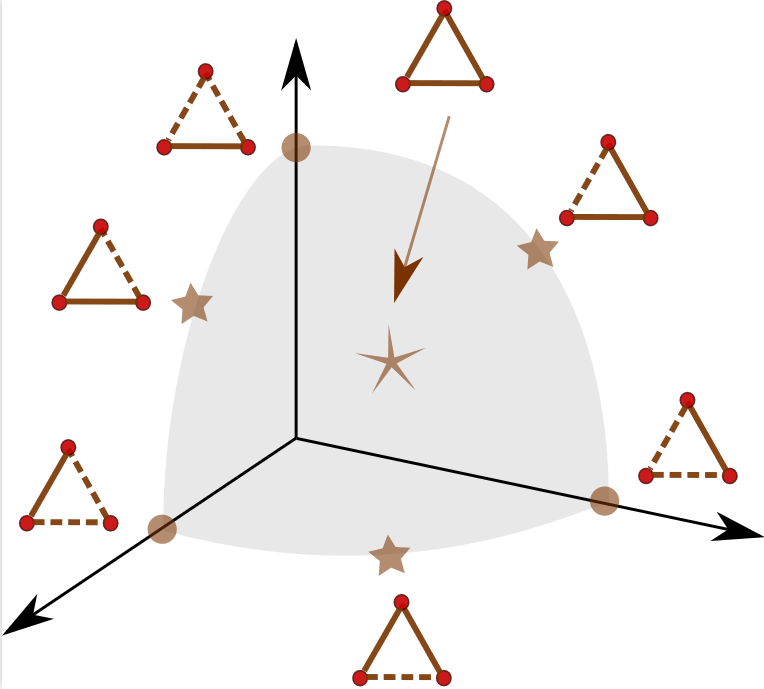
We defined in [hal-03910825] a novel embedding space for binary undirected graphs, the Currents Spaces of Graphs. We represent simple graphs on n vertices by 1-forms over a complete graph K_n. It is shown that these 1-forms lie on a hypersphere in the Hilbert space L^2 (\Omega^1_{K_n}) of all 1-forms and the round metric induces a natural distance metric on graphs. The metric itself reduces to a global spherical Jaccard-type metric which can be computed from edge-list data alone. The structure of the graph space embedding for three vertices is illustrated in the figure.
Lastly, we describe the global structure of the 1-forms representing graphs and how these can be exploited for the statistical analysis of a sample of graphs.
The Measurement and Analysis of Shape: An Application of hydrodynamics and probability theory
James Benn, Stephen Marsland.
A de Rham p-current can be viewed as a map (the current map) between the set of embeddings of a closed p-dimensional manifold into an ambient n-manifold and the set of linear functionals on differential p-forms. We demonstrate that, for suitably chosen Sobolev topologies on both the space of embeddings and the space of p-forms, the current map is continuously differentiable, with an image that consists of bounded linear functionals on p-forms. Using the Riesz representation theorem we prove that each p-current can be represented by a unique co-exact differential form that has a particular interpretation depending on p.
Embeddings of a manifold can be thought of as shapes with a prescribed topology. Our analysis of the current map provides us with representations of shapes that can be used for the measurement and statistical analysis of collections of shapes. We consider two special cases of our general analysis and prove that: (1) if p=n-1 then closed, embedded, co-dimension one surfaces are naturally represented by probability distributions on the ambient manifold; and (2) if p=1 then closed, embedded, one-dimensional curves are naturally represented by fluid flows on the ambient manifold. In each case we outline some statistical applications using an \dot{H}^{1} and L^{2} metric, respectively. [hal-03556752]
Tangent phylogenetic PCA
Morten Pedersen, Stefan Sommer, Xavier Pennec.
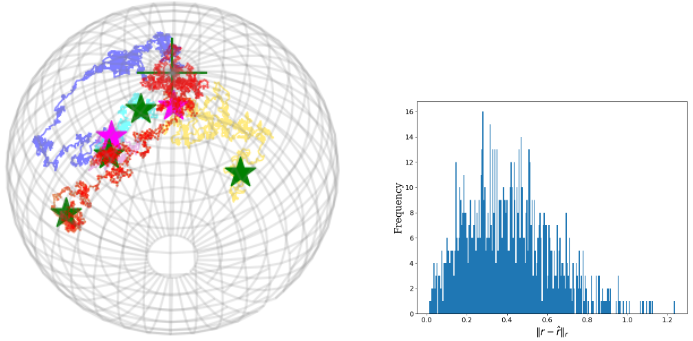
Phylogenetic PCA (p-PCA) is a well-known version of PCA for observations that are leaf nodes of a phylogenetic tree. The method works on Euclidean data, but in evolutionary biology there is a need for applying it to data on manifolds, particularly shape-trees. We provide in [hal-03842847] a generalization of p-PCA to data lying on Riemannian manifolds, called Tangent p-PCA. The figure illustrates step 1 of our method, consisting of estimating the unknown root node of the phylogenetic tree.
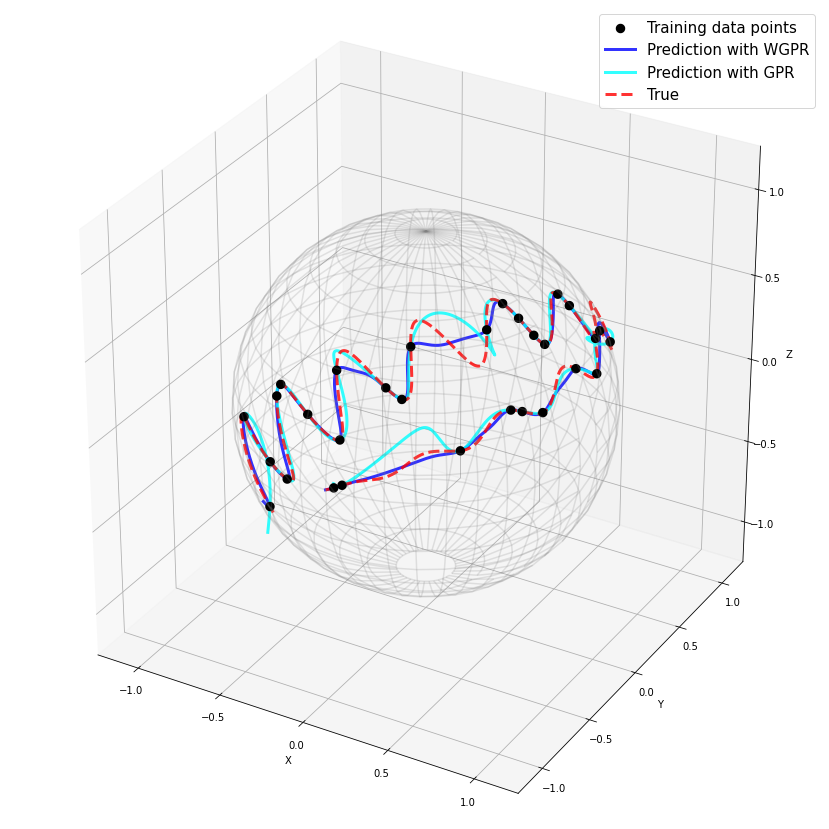
Wrapped Gaussian Process Regression on Riemannian Manifolds
Tom Szwagier, Arthur Pignet.
This work focuses on the implementation in the python library Geomstats of wrapped Gaussian process regression on Riemannian manifolds. This work won the second prize from the ICLR Computational Geometry &Topology Challenge associated to the ICLR 2022 Workshop on Geometrical and Topological Representation Learning. The challenge and its submissions are summarized in the white paper [hal-03903044] and the code is available on the challenge repository.
Geometries of covariance and correlation matrices
Yann Thanwerdas, Xavier Pennec.
In [hal-03414887], we use the principles of deformed metrics and balanced metrics to:
1. introduce Mixed-Power-Euclidean metrics which encompass the Euclidean, affine-invariant, log-Euclidean and BKM metrics;
2. relate the MPE metrics to the (u,v)-divergences of Information Geometry;
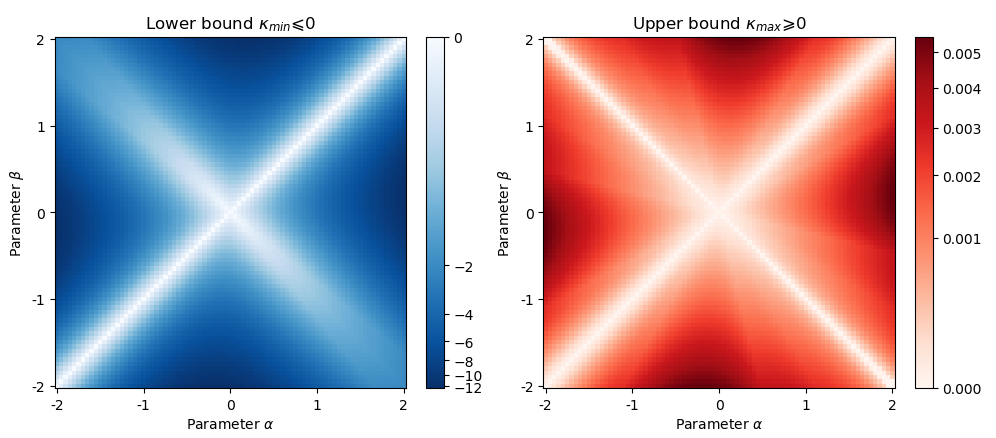
3. compute the curvature (see bounds on the figure).
In [tel-03698752], we further:
1. introduce convenient metrics on correlation matrices of full rank;
2. characterize the Bures-Wasserstein geodesics on covariance matrices.
